What is Pattern Formation?
Patterns form when an initially unstructured physical system develops a structured appearance, usually through the change of some control parameter. At Dickinson, Professor David Jackson maintains an active research program in pattern formation that typically revolves around the interfacial instabilities of a magnetic fluid (a ferrofluid) under the application of a magnetic field. A ferrofluid is a liquid with ~10 nm magnetic spheres that are coated with a surfactant and suspended in a carrier fluid. In the absence of a magnetic field a ferrofluid behaves just like a normal liquid. But when subjected to a magnetic field, the tiny dipoles in the fluid align with the applied field resulting in a magnetic pressure that leads to a number of interesting instabilities.
Most of our work is done in a quasi-two-dimensional geometry that consists the fluid trapped between two closely-spaced glass plates (a Hele-Shaw cell). Shown here is a Hele-Shaw cell with some ferrofluid drops inside.

The Hele-Shaw cell is then placed subjected to an external magnetic field that is supplied by a pair of Helmholtz coils. The evolution of the ferrofluid is then captured with a digital video camera. The following picture shows the entire setup.

In this geometry, the ferrofluid initially takes the shape of a circle. But when a magnetic field is applied, the fluid evolves into a complex branched structure whose features depend on the details of how the field was applied. Shown below is a snapshot of a typical ferrofluid evolution (click on the image to see a movie of this evolution).

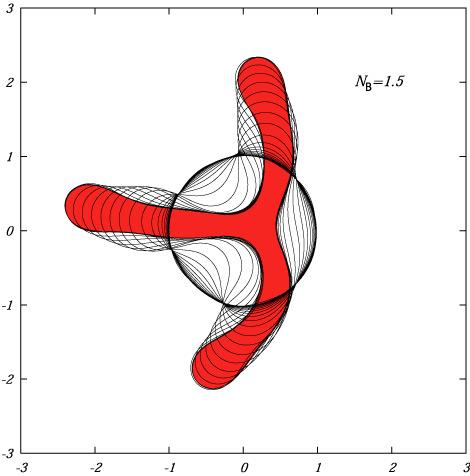
In addition to physical experiments, we also perform numerical experiments (computations) of these systems. One way to view these computational evolutions is to make a time-overlay image in which the outline of the ferrofluid is periodically printed. The following time-overlay image shows one such evolution. In this simulation, the initial configuration is a circle and the final state is the branched structure (colored red for clarity).
Here is a sampling of publications arising from this research:
"Hysteresis and multiple stable configurations in a magnetic fluid system," D. P. Jackson, J. Phys.: Condens. Matter 20, 204140 (5pp) (2008).
"Confined ferrofluid droplet in crossed magnetic fields," D. P. Jackson and J. A. Miranda, Eur. Phys. J. E23, 389-396 (2007).
"Width of a ferrofluid finger: Hysteresis and a double energy minimum," N. J. Hillier and D. P. Jackson, Phys. Rev. E75, 036314 (7pp) (2007).
"Theory, Experiment, and Simulations of a Symmetric Arrangement of Quasi-Two-Dimensional Magnetic Fluid Drops," D.P. Jackson, J. Magn. Magn. Mater. 289, 188-191 (2005).
"Adhesion Phenomena in Ferrofluids," J.A. Miranda, R.M. Oliveira, and D.P. Jackson, Phys. Rev. E70, 036311 (2004).
"Orientational Preference and Predictability in a Symmetric Arrangement of Magnetic Drops," D.P. Jackson, Phys. Rev. E68, 035301(R) (2003).
"Controlling Fingering Instabilities in Rotating Ferrofluids," D.P. Jackson and J.A. Miranda, Phys. Rev. E67, 017301 (2003).
"Energetics and Interacting Magnetized Domains," D.P. Jackson and B. Gantner, Phys. Rev. E64, 056230 (2001).